728x90
반응형
4.3.1 서포트 벡터 머신
- 지도 학습 머신 러닝 모델이며, 주로 분류와 회귀분석에 사용
- 마진으로 최대화할 수 있는 결정 경계선을 찾아 입력된 데이터가 어느 카테고리에 속할지 판단하는 알고리즘
- 결정 경계에 따라 선형과 비선형 분류 모델로 정의
- 핵심 용어 : 결정 경계, 서포트 벡터, 마진, 비용, 초평면
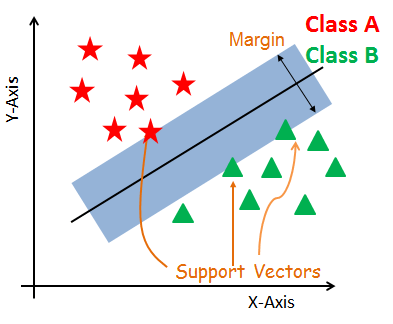
4.3.1.1 서포트 벡터란?
- 서포트 벡터(Support Vector) → 2차원 공간 상에 나타나는 데이터 포인트를 의미 → 쉽게 말해, 입력되는 데이터를 표현한 것
4.3.1.2 결정 경계
- 결정 경계 → 주어진 데이터를 통해 만들어지는 모델로, 서포트 벡터 머신 학습의 궁극적인 목적인 이 결정 경계를 찾는 것 → 결정 경계의 차원은 데이터의 벡터 공간의 차원보다 한 차원 낮음
- N: 데이터의 벡터 공간차원일때,
결정 경계 차원 = N -1
4.3.1.3 마진이란?
- 마진(margin) → 서포트 벡터와 결정 경계 사이의 거리 → SVM은 이 마진을 최대로 하는 결정 경계를 찾는 것이 목표 → 즉, 통계적으로 허용하는 범위에서 성능이
4.3.1.4 비용이란?
- 비용 (cost, loss) → 어떤 모델의 성능을 평가할 때 사용되는 중요한 변수 → SVM에서는 비용(C)라고 정의
- 비용의 모델 평가
[주어진 데이터에 대해!!]
*비용이 낮으면 → 과소 적합의 위험 (모델의 목표대로 잘 찾지 못함)
*비용이 높으면 → 과대 적합의 위험 (TEST 데이터에 대해 잘 찾지 못함)
*결론적으로 적절한 비용 값을 찾는 과정이 상당히 중요하고, 이것이 학습일 것이다. - SVM의 비용
- SVM에서의 비용은 어떤 의미를 가질까??
[주어진 데이터에 대해!!]
비용이 낮다 → 마진을 최대한 높이고 학습 에러율을 증가시키는 결정 경계선 생성
비용이 높다 → 마진은 낮고, 학습 에러율은 감소하는 결정 경계선 생성
결론적으로, SVM은 주어진 데이터로 결정 경계선을 생성하여 분류 및 회귀 분석을 하고, 적절한 비용을 가지는 모델을 찾아가는 것이 목표!
이때, 마진이 낮다는 것은 다른 데이터에 대해 적용되기 힘들다는 것이니, 과대 적합에 부합하는 내용이 되고 마진이 높다는 것은 학습 데이터에 대해서도 잘 처리하지 못하는 것이기에 과소 적합과 부합된다고 볼 수 있다.
4.3.1.5 서포트 벡터 머신의 사용하기
- 서포트 벡터 머신, 즉 결정 경계선을 만들기 위한 필요한 작업 및 입력 변수들이 있음
- 선형 SVM: 커널을 사용하지 않고 데이터를 분류, 비용(C)을 조절해서 마진의 크기 조절 (참조 4.3.1.4 비용이란?)
- 커널 트릭: 선형 분리가 주어진 차원에서 불가능할 경우 고차원으로 데이터를 옮기는 효과를 통해 결정 경계를 찾음 → 주요 입력 변수 : 비용, gamma, 마진
[커널 트릭 좀 더 알아보기]
'''
커널 트릭은 "선형 분리"가 불가능할 경우에 데이터의 공간을 저 차원에서 고차원으로 매핑해줌으로써 결정 경계 모델을 찾음
'''
[커널 트릭 사용하기]
커널 트릭의 SVM을 실습 시에 중요한 변수는 다음과 같다.
>> 비용 : 마진 너비 조절 변수, 클수록 마진 너비가 좁아지고 작을수록 마진 너비가 넓어짐
>> 감마 : 커널의 표준 편차 조절 변수, 작을수록 경계 결정선이 완만해지고, 클수록 결정 경 계선이 굴곡을 가짐
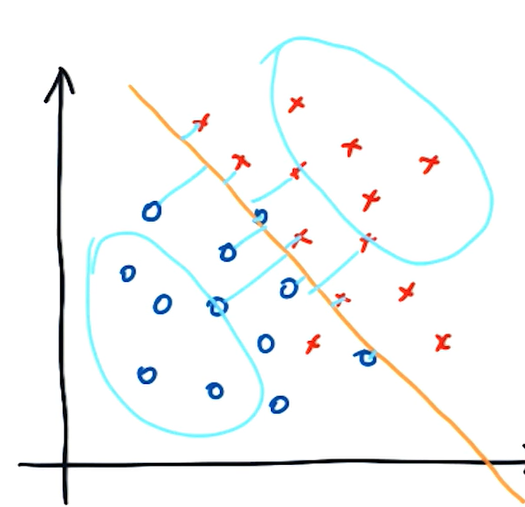
결론적으로 Gamma가 크면 decision boundary는 더 굴곡지고, Gamma가 작으면 decision boundary는 직선에 가깝다.

728x90
반응형
'AI Study' 카테고리의 다른 글
| [AI Study] ImageDataGenerator 사용하여 CIFAR-10 분류하기 (0) | 2021.06.22 |
|---|---|
| [머신러닝] 의사결정 트리 (0) | 2021.04.30 |
| [AI Study] 인공지능 강의 #2(Andrew.Ng). 경사 하강법이란? (0) | 2021.03.04 |
| [AI Study] 인공지능 실습 #1. KERAS를 이용하여 MNIST 학습하기 (0) | 2021.03.03 |
| [AI Study] 인공지능 강의 #1(Andrew.Ng). 로지스틱 회귀란? 로지스틱 회귀의 비용함수란? (0) | 2021.02.25 |
