#1. Andrew Ng. Lecture.C1W2L04
강의 출처 : www.youtube.com/channel/UCcIXc5mJsHVYTZR1maL5l9w
DeepLearningAI
Welcome to the official DeepLearning.AI YouTube channel! Here you can find the videos from our Coursera programs on machine learning as well as recorded events. DeepLearning.AI was founded in 2017 by machine learning and education pioneer Andrew Ng to fill
www.youtube.com
본업 이외에 따로 무엇가를 준비한다는 것은 쉬운일은 아닌거 같다. 하지만, 꾸준히 하자!
01. Lecture 10. Gradient Descent
- 강의 목적 - "경사 하강법 (Gradient Descent)" 알고리즘을 사용한, 매개변서 w, b를 훈련세트에 학습시키는 방법.
- 이전 강의의 연장선으로, 로지스틱회귀 함수의 경사하강법에 대한 설명.

로지스틱 회귀법의 "시그모이드 함수" 를 예로 들어 설명합니다.
(그림 1의 첫번째 식) "시그모이드 함수"의 표현 식입니다.
(그림 1의 두번째 식) "비용함수"를 J라 할 때, 비용함수 J는 w, b에 대한 함수가 됩니다.
이 함수 J는 "손실함수의 평균"으로 정의합니다. 즉, 손실함수와 비용함수는 목적은 같지만 약간의 의미는 다릅니다.
결국, m개의 데이터셋이 있다면 각 데이터셋의 손실함수를 계산한 값의 평균이 "비용함수" 로 정의됩니다.
이는 훈련셋이 얼마나 참값과 예측값이 맞는지에 대한 측정이 가능하죠.
(그림 1의 그래프) 두 가로축은 w,b에 대한 정의가 된 축입니다. 세로축은 비용함수 J에 의한 (w,b)의 출력 값이 되겠죠.
J함수가 저 그림에 따른 모양이라면, 어느한점 (w,b)에서 가장 적은 최소값을 찾으려 할 것입니다.
그것이 알고리즘이고, 비용함수 J가 아래로 볼록한(convex)한 모양이라는 것이 로지스틱 회귀가 적용에 적절한 비용
함수가 된다는 것을 의미하고, 이대의 w, b가 적절한 파라미터라고 할 수 있겠습니다.
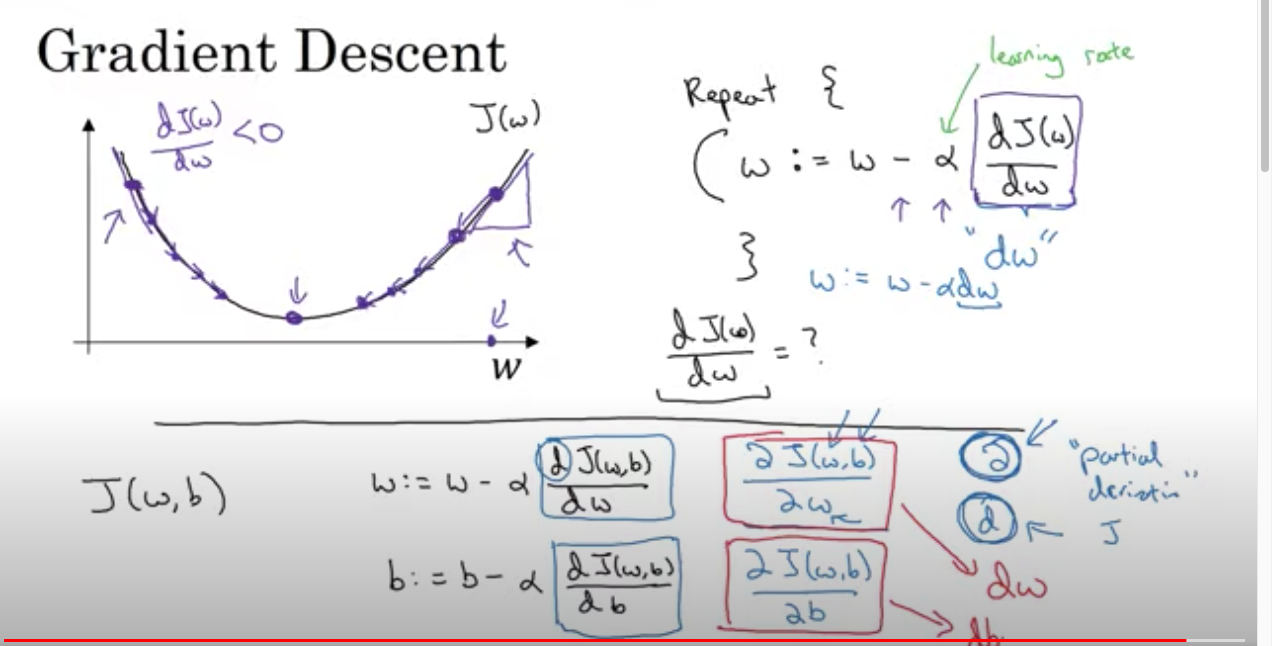
결국에는 비용함수 J의 목적은 최소 값을 찾는 것이고, 이 최소값을 찾아나가는 방법이 "경사하강법"입니다.
그리고, 비용함수 J가 최소 값일 때 w, b가 적절한 파라미터이므로 이 w, b를 갱신해가며 비용함수 J를 따라 함수값
이 최소 값이 되는 w, b를 찾아야겠죠.
그림2가 이에 대한 내용입니다.
경사하강법을 본다면 결국 w를 갱신해나가는 것이고, 이 갱신은 기존 w에서 J(w)의 기울기 값에서 a(학습률)의 곱
을 빼 는 것으로 갱신해나간다고 합니다.
즉, 기울기가 양일때는 w가 작아지는, 기울기가 음일때는 w가 커지면서 J(w)가 작은 global 미니마를 찾는것이죠.
여기서 중요한 것은 우리가 w,b를 경사하강법으로 J(w,b)가 최소가 되는 w,b를 찾는 것이다.
어떻게?? 미분으로!!
그림 2의 모든 식들이 해당 내용 w := w - a* dJ(w,b)/dw b := b - a* dJ(w,b)/db - 우리는 천천히 이해할 수 있습니다!
다음에는 미분으로 어떻게 찾아가는지 공부하면서 미분의 의미도 정립해보도록 하겠습니다.
'AI Study' 카테고리의 다른 글
| [AI Study] ImageDataGenerator 사용하여 CIFAR-10 분류하기 (0) | 2021.06.22 |
|---|---|
| [머신러닝] 의사결정 트리 (0) | 2021.04.30 |
| [머신러닝] 서포트 벡터 머신(SVM) (0) | 2021.04.29 |
| [AI Study] 인공지능 실습 #1. KERAS를 이용하여 MNIST 학습하기 (0) | 2021.03.03 |
| [AI Study] 인공지능 강의 #1(Andrew.Ng). 로지스틱 회귀란? 로지스틱 회귀의 비용함수란? (0) | 2021.02.25 |

