#1. Andrew Ng. Lecture.C1W2L01 ~ C1W2L03
강의 출처 : www.youtube.com/channel/UCcIXc5mJsHVYTZR1maL5l9w
01. Logistic Regression
- 강의 목적 - "로지스틱 회귀가 어떤 것인가" 에 대한 간략한 전달
- "로지스틱 회귀"는 "지도학습 문제"에서 출력 레이블 y가 0 or 1 일 경우 즉, 이진 분류에 사용되는 알고리즘

예를들어, 고양이 사진인지 아닌지 구분하는 경우라면? x라는 입력이 주어지면, y의 예측값을 출력하는 알고리즘이 필요
할 것 즉, x는 고양이 사진이고, y의 예측값은 고양이 사진일 확률 일것 문제는, 입력 x와 파라미터 w,b가 주어졌을
때, 어떻게 y의 예측값을 출력 할 수 있을까?
잘 안되는 방법은 w*x +b 와 같은 선형식으로 두는 것. 왜??
선형함수는 음수도 가질 수있기에, 이진 분류에는 좋은 방법이 아니다.
왜냐하면, 예측 값인 y는 확률로 항상 0<y<1 값을 가져야하기 때문!! 그렇기 때문에 0과 1로 표현이 잘 되어질 수 있는
활성 함수인 "시그모이드 함수" 를 주로 적용한다.

위 그림은 "시그모이드 함수" 그래프와 식을 나타낸다. 이를 보면 알 수 있듯이, z가 양의 값으로 클수록 z의 함수 값은 1
에, z가 음의 값으로 클수록 z의 함수 값은 0에 수렴한다.
그러므로 로지스틱 회귀를 구현할때, y가 1이 될 확률을 잘 예측하도록 파라미터 w,b를 학습해야 한다.
02. Lecture 09. Logistic Regression Cost Function
- 강의 목적: 파라미터 w, b를 학습하려면, 비용함수의 정의가 필요. "로지스틱 회귀"를 학습할 수 있는 비용함수에 대해 알아보자.
- 손실함수(loss function), 비용 함수 (cost function), 목적 함수 (objective function): 머신러닝을 통한 예측값이 실제값과 차이(오차)와 관련한 식(equation)
- 예측값과 실제값의 오차를 최소화하려 하면 비용함수 혹은 손실함수라 함. 즉, 비용함수는 예측값의 오차를 최소화하기 위해 최적화된 식이어야 함

위 식에 대해 말해보자면, i번째 y의 예측값은 w*x(i) + b의 시그모이드이며, 이때 시그모이드 함수는 첫 번째 줄의
where 이후의 식으로 정의가 된다. 즉, w*x(i) + b가 i번째 z로 치환이 된다고 보면 된다.
1~m개의 주어진 훈련 데이터를 w, b를 찾아 학습할때, 우리가 원하는 값은 i번째 y의 예측값이 훈련 세트에 포함된 i번
째 y의 참값과 가까워지도록 하는 것.
이를 측정 할 수 있는 것이 손실함수(=오차함수=비용함수)이다. 손실함수를 L이라고 부르고, y^ = 예측값, y = 참값이
라 할때, 1/2(y^ - y)^2가 손실함수로 표현될 수 있으나, "로지스틱 회귀" 에서는 적절한 손실함수가 아니다.
여기서 명심할 것은 y의 예측값과 y 참값의 오차가 얼마나 큰지를 측정하는 것이 "손실함수"
- 그렇다면, 로지스틱 회귀법에서 시그모이드 함수의 적절한 손실함수는 ??다음과 같이 표현 할 수 있다.

그 이류를 이해한대로 적어보자!
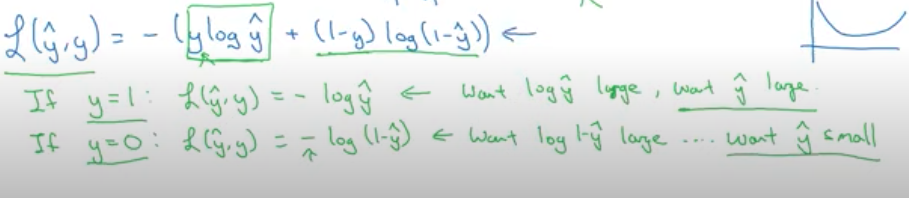
손실함수는 최소화 되어야하는 것을 전제로 한다.
y^ 이 예측값, y가 참값이라 할때 y^는 로지스틱 회귀 함수를 따른다.
y= 1 경우) 손실함수 L= -log(y의 예측값)이 되고, 우리는 예측값이 1 이 되길 원하므로 손실함수는 최소가 되길 원할
것. 그럴려면, y의 예측값(y^)이 최대 값이 되도록 그려져야하고, y^은 로지스틱 회귀 함수를 따르기에 1에 수렴하도로
증가할 것이다.
반면에, y = 0 경우) 손실함수 L = -log(1-y의 예측값)이 되고, 우리는 예측값이 0 이 되길 원하므로 손실함수는 최소가
되길 원할 것이고, 그러므로, 1-y의 예측값이 최대 값이 되도록그려져야하고, y^는 최소가 되도록 가야할 것이다.
y^는 로지스틱 회귀 함수를 따르기에 0에 수렴하도록 감소할 것이다.
정말 어렵지만, 조금씩 알아가고 있는것 같아 기쁘다! 꾸준히 하자!
'AI Study' 카테고리의 다른 글
| [AI Study] ImageDataGenerator 사용하여 CIFAR-10 분류하기 (0) | 2021.06.22 |
|---|---|
| [머신러닝] 의사결정 트리 (0) | 2021.04.30 |
| [머신러닝] 서포트 벡터 머신(SVM) (0) | 2021.04.29 |
| [AI Study] 인공지능 강의 #2(Andrew.Ng). 경사 하강법이란? (0) | 2021.03.04 |
| [AI Study] 인공지능 실습 #1. KERAS를 이용하여 MNIST 학습하기 (0) | 2021.03.03 |

